R을 공부하는 이유는 당연히 통계분석을 잘하기 위해서이다. 따라서, R을 공부한다는 것은 통계학에 대한 기본 지식이 있거나, 아니면 통계학에 대한 기본적인 내용을 같이 공부한다는 말일 것이다.
통계학에 대한 공부를 병행하면서 통계 실습에 대한 부분을 R로 진행하여 기록에 더할까 한다.
2019/12/22 - [공부하記/통계학] - 통계학 기초 - 자료의 생성, 모집단과 표본, 위치 측도와 산포 측도
어느 과목에 대한 100명의 시험성적을 예제 데이터로 사용한다.
# Plot
> plot(exam)


summary( ) 함수를 통해 데이터의 기본 정보를 확인할 수 있다.
Minimum(최소값), 1st Quartile(1사분위값), Median(2nd Quartile)(중간값), 3rd Quartile(3사분위값), Maximum(최대값)
# exam의 기본 정보를 확인한다.
> summary(exam)

위치 측도
위치 측도(location parameters) : 모집단/표본에 속한 특성 값들의 대략적인 크기를 나타내는 측도
# 표본 평균
> mean(exam)
# 중앙값
> median(exam)
# p% 분위수
> p <- 0.2
> quantile(exam, p)

산포 측도
산포 측도(scale parameters) : 모집단/표본에 속한 특성 값들이 얼마나 멀리/가까이 퍼져있나를 나타내는 측도
# 표본 분산
> var(exam)
# 표본 표준 편차
> sd(exam)
# 중앙 절대 편차
> mad(exam)
# 사분위수 범위
> IQR(exam)

이상치에 대한 민감도 관찰
> set.seed(100)
# rnorm( ) 함수로 표준 정규분포에 따르는 난수를 생성한다.
> data1 <- rnorm(100, 0, 1) # 평균이 0이고, 표준 편차가 1인 난수 100개를 생성한다.
# 이상치값 변환
> data2 <- data1
> data2[100] <- data1[100] * 1000 # data2의 마지막 100번째 값을 이상치로 만든다

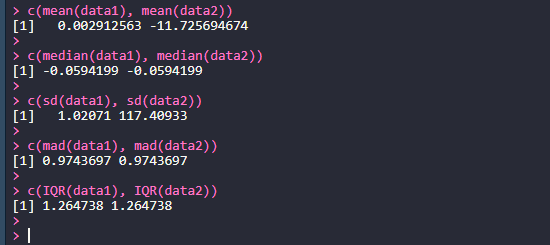
이상치 변환 후에 여러 측도들을 비교해 보면, 단 하나의 이상치에 평균값과 표준편차는 크게 변하지만(민감도가 높다), 중앙값과 중앙 절대 편차, 사분위수 범위는 변화가 없음(민감도가 낮다)을 알 수 있다
> c(mean(data1), mean(data2))
> c(median(data1), median(data2))
> c(sd(data1), sd(data2))
> c(mad(data1), mad(data2))
> c(IQR(data1), IQR(data2))
> Q1 <- quantile(data1, seq(1, 100) / 100)
> Q2 <- quantile(data2, seq(1, 100) / 100)
> plot(Q1, Q2, type = "b")


분포의 모양에 따른 Mean(평균값)과 Median(중앙값)의 비교
> set.seed(1000)
# rbeta(n, shape1, shape2) : shape1, ahape2 파라미터르 통한 n개의 베타 난수 생성
> x1 <- rbeta(10000, 2, 4)
> x2 <- rbeta(10000, 5, 5)
> x3 <- rbeta(10000, 4, 2)
# 각 표본에서의 평균값과 중앙값
> c(mean(x1), mean(x2), mean(x3))
> c(median(x1), median(x2), median(x3))
# 각 표본에서의 표준편차
> c(sd(x1), sd(x2), sd(x3))
> c(mad(x1), mad(x2), mad(x3))


> par(mfrow = c(2, 2))
> hist(x1)
> hist(x1, nclass = 5)
> hist(x1, nclass = 10)
> hist(x1, xlim = c(0.005, 1.2)) #xlim : 구간 정의
> stem(x1)


> par(mfrow = c(3, 2))
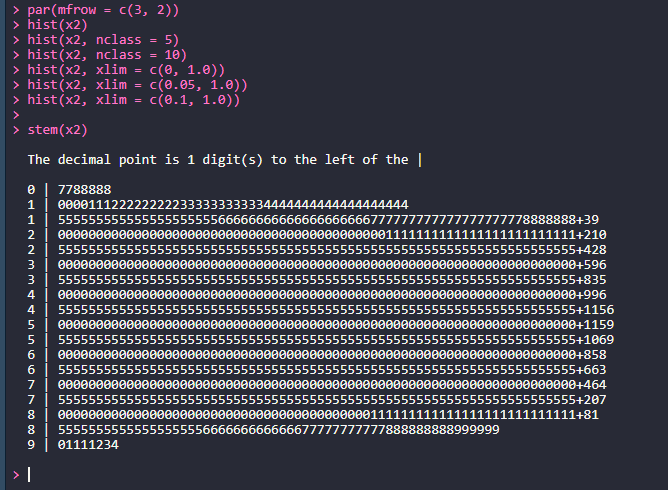
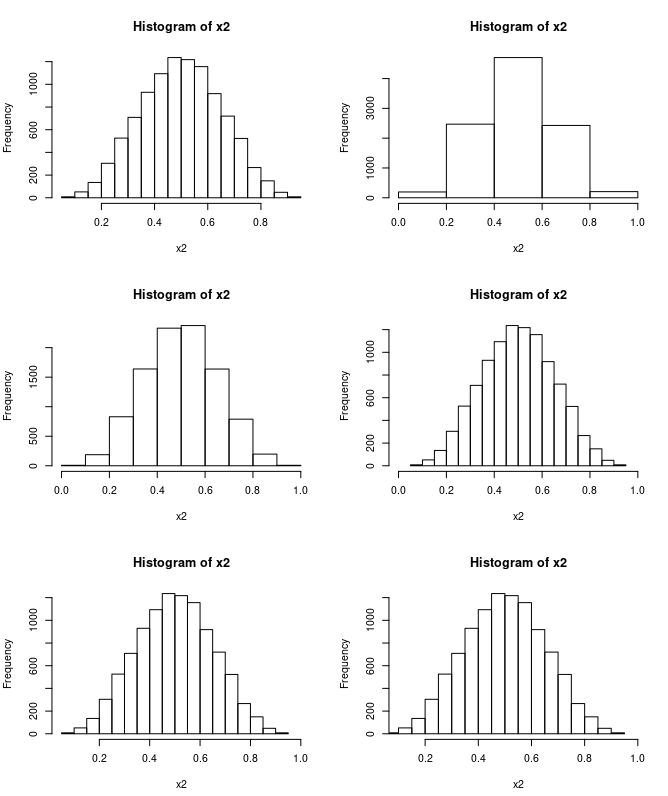
> hist(x2)
> hist(x2, nclass = 5)
> hist(x2, nclass = 10)
> hist(x2, xlim = c(0, 1.0))
> hist(x2, xlim = c(0.05, 1.0))
> hist(x2, xlim = c(0.1, 1.0))
> stem(x2)
> hist(x3)
> hist(x3, nclass = 5)
> hist(x3, nclass = 10)
> hist(x3, xlim = c(0.05, 1.0))
> hist(x3, xlim = c(0.05, 1.2))
> stem(x3)


왜도와 첨도
자료의 대칭성을 알아보는 측도인 왜도(skewness)와 정규 분포 대비 봉오리의 높이를 알아보는 측도인 첨도(kurtosis)를 알아보기 위해서는 'fBasic' 패키지가 필요하다.
> install.packages("fBasics")
> library(fBasics)


왜도의 값이 0이면 정규분포, 0보다 크면 오른쪽으로 긴꼬리 분포, 0보다 작으면 왼쪽으로 긴꼬리 분포를 나타낸다.
첨도의 값이 0이면 정규분포와 같은 높이, 0보다 크면 정규분포보다 뾰족하고, 0보다 작으면 납작함을 나타낸다.
# x1
> kurtosis(x1) # 첨도
> skewness(x1) # 왜도
# x2
> kurtosis(x2)
> skewness(x2)
# x3
> kurtosis(x3)
> skewness(x3)

> boxplot(x1)
> boxplot(x2)
> boxplot(x3)
> boxplot(x1, x2, x3)


'해보記 > R' 카테고리의 다른 글
| <記> R 상관계수와 공분산 (0) | 2020.01.01 |
|---|---|
| <記> R 스타일 가이드 (0) | 2019.12.30 |
| <記> R 데이터 반복문 - for, while, repeat, apply, aggregate (1) | 2019.12.18 |
| <記> R 데이터 조건문 - if/ifelse, switch (0) | 2019.12.18 |
| <記> R 함수 - 기타 (1) | 2019.12.17 |